Introduction to Flexible Clustering of (Mixed-With-)Ordinal Data

Source: ../vignettes/Intro2Flexord.Rmd

Package description and contents

Package flexord is an add on-package to packages flexclust and flexmix that provide suites for partitioning and model-based clustering with flexible method switching and comparison.

We provide additional distance and centroid calculation functions, and additional model drivers for component distributions that are tailored towards ordinal, or mixed-with-ordinal data. These new methods can easily be plugged into the capabilities for clustering provided by flexclust and flexmix.

By plugging them into the flex-scheme, they can be used for:

The new methods provided are:
Clustering Type Function Type Function Name Method Scale Assumptions NA Handling Source
Partitioning (K-centroids) distance distSimMatch Simple Matching Distance nominal not implemented Kaufman and Rousseeuw (1990), p. 19
distGDM2 GDM2 distance for ordinal data ordinal not implemented Walesiak and Dudek (2010); Ernst et al. (2025)
distGower Gower’s distance mixed-with-ordinal upweighing of present variables Kaufman and Rousseeuw (1990), p. 32-37
centroid centMode Mode as centroid nominal not implemented Weihs et al. (2005); Leisch (2006)
centMin Factor level with minimal distance as centroid nominal/ordinal not implemented Ernst et al. (2025)
centOptimNA Centroid calculation by general purpose optimizer numeric complete-case analysis Leisch (2006)
wrapper kccaExtendedFamily Creates a kccaFamily object pre-configured for kModes-, kGDM2- or kGower clustering
Model-based driver FLXMCregnorm Regularized multivariate normal distribution numeric not implemented Fraley and Raftery (2007); Ernst et al. (2025)
FLXMCregmultinom Regularized multivariate multinomial distribution nominal not implemented Galindo Garre and Vermunt (2006); Ernst et al. (2025)
FLXMCregbinom Regularized multivariate binomial distribution ordinal not implemented Ernst et al. (2025)
FLXMCbetabinomial Regularized multivariate beta-binomial distribution ordinal not implemented Kondofersky (2008); Ernst et al. (2025)

Example 1: Clustering purely nominal data

We load necessary packages and set a random seed for reproducibility.

library("flexord")
library("flexclust")
library("flexmix")
set.seed(1111)

As an example for purely nominal data, we will use the classic Titanic data set:

titanic_df <- data.frame(Titanic)
titanic_df <- titanic_df[rep(1:nrow(titanic_df), titanic_df$Freq), -5]
str(titanic_df)
#> 'data.frame':    2201 obs. of  4 variables:
#>  $ Class   : Factor w/ 4 levels "1st","2nd","3rd",..: 3 3 3 3 3 3 3 3 3 3 ...
#>  $ Sex     : Factor w/ 2 levels "Male","Female": 1 1 1 1 1 1 1 1 1 1 ...
#>  $ Age     : Factor w/ 2 levels "Child","Adult": 1 1 1 1 1 1 1 1 1 1 ...
#>  $ Survived: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...

Partitioning approach

We can conduct K-centroids clustering with the kModes algorithm directly on the data frame1:

kcca(titanic_df, k = 4, family = kccaExtendedFamily('kModes'))
#> kcca object of family 'kModes' 
#> 
#> call:
#> kcca(x = titanic_df, k = 4, family = kccaExtendedFamily("kModes"))
#> 
#> cluster sizes:
#> 
#>    1    2    3    4 
#>  140  396  287 1378

Let us assume that for some reason we are unhappy with the mode as a centroid, and rather want to use an optimized centroid value, by choosing the factor level for which Simple Matching distance2 is minimal:

kcca(titanic_df, k = 4,
     family = kccaFamily(dist = distSimMatch, 
                         cent = \(y) centMin(y, dist = distSimMatch,
                                             xrange = 'columnwise')))
#> kcca object of family 'distSimMatch' 
#> 
#> call:
#> kcca(x = titanic_df, k = 4, family = kccaFamily(dist = distSimMatch, 
#>     cent = function(y) centMin(y, dist = distSimMatch, xrange = "columnwise")))
#> 
#> cluster sizes:
#> 
#>   1   2   3   4 
#> 369 737 317 778

This already showcases one of the advantages of package flexclust: As the name suggests, we are quickly able to mix and match our distance and centroid functions, and quickly create our own K-centroids algorithms.

Furthermore, flexclust allows us to decrease the influence of randomness via running the algorithm several times, and keeping only the solution with the minimum within cluster distance. This can be done for one specific number of clusters k or several values k:

titanic_dm <- data.matrix(titanic_df)
stepFlexclust(titanic_dm, k = 2:4, nrep = 3, 
              family = kccaExtendedFamily('kModes')) 
#> 2 : * * *
#> 3 : * * *
#> 4 : * * *
#> stepFlexclust object of family 'kModes' 
#> 
#> call:
#> stepFlexclust(x = titanic_dm, k = 2:4, nrep = 3, family = kccaExtendedFamily("kModes"))
#> 
#>   iter converged distsum
#> 1   NA        NA  651.50
#> 2  200     FALSE  413.50
#> 3  200     FALSE  278.75
#> 4  200     FALSE  246.00

The output above shows the solutions with lowest within cluster distance out of 3 runs for 2 to 4 clusters, in comparison to 1 big cluster. However, none of the algorithms converged. Presumably this is due to observations which have the same distance to two centroids and which are randomly assigned to one of the two centroids, implying that the partitions are still changing in each iteration, even if the centroids do not change.

Selecting a suitable number of clusters based on the output of stepFlexclust might be still difficult. This is where bootFlexclust comes in. In bootFlexclust, nboot bootstrap samples of the original data are drawn, on which stepFlexclust is performed for each k. This results in k\(\times\)nboot best out of nrep clustering solutions obtained for each bootstrap data set. Based on these solutions cluster memberships are predicted for the original data set, and the stability of these partitions is tested via the Adjusted Rand Index (Hubert and Arabie 1985):

(nom <- bootFlexclust(titanic_dm, k = 2:4, nrep = 3, nboot = 5, 
                      family = kccaExtendedFamily('kModes')))
#> An object of class 'bootFlexclust' 
#> 
#> Call:
#> bootFlexclust(x = titanic_dm, k = 2:4, nboot = 5, nrep = 3, family = kccaExtendedFamily("kModes"))
#> 
#> Number of bootstrap pairs: 5

Note that ridiculously few repetitions are used for the sake of having a short run time. Clearly nboot should be increased in applications.

The resulting ARIs can be quickly visualized via a predefined plotting method:

plot(nom)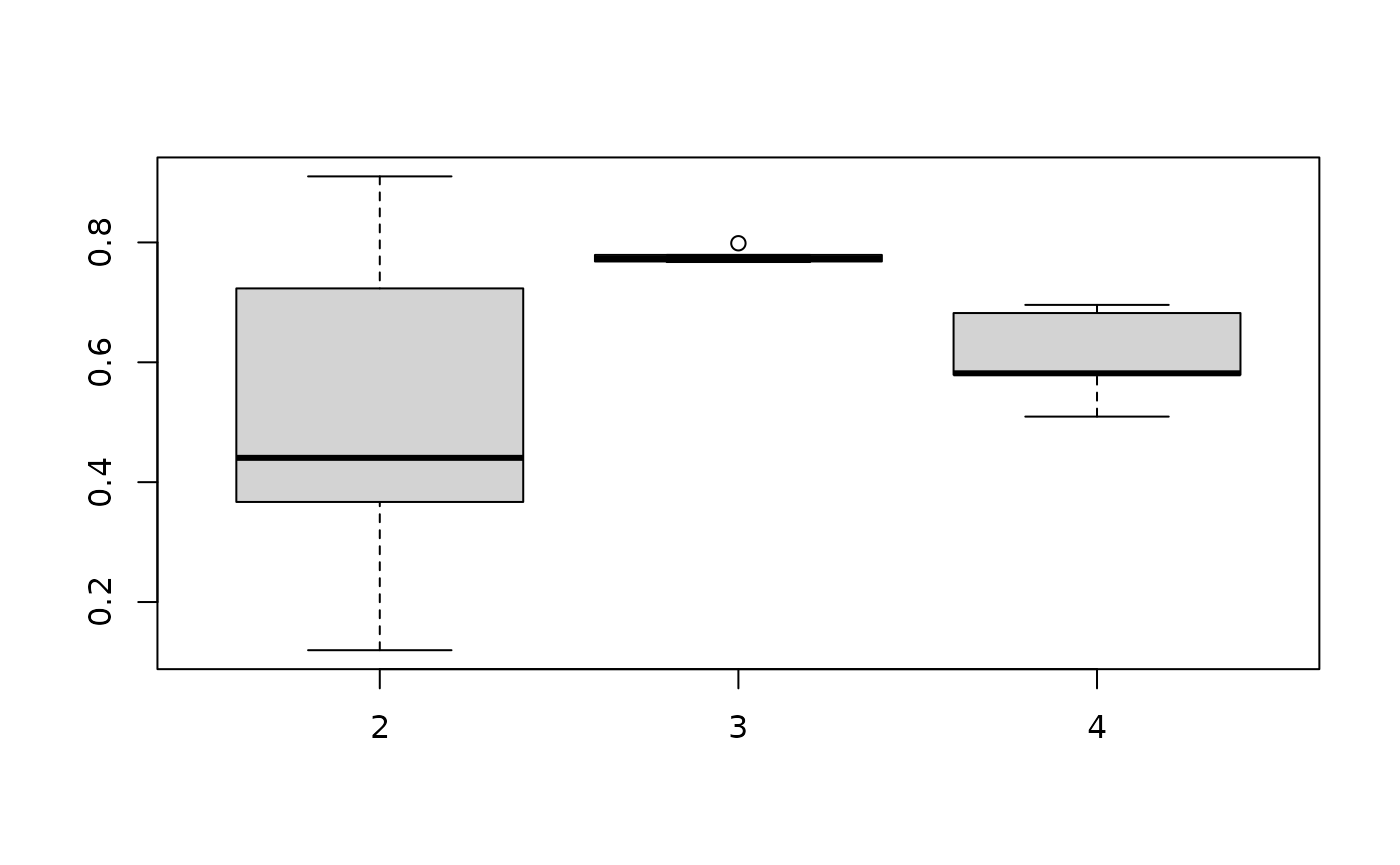

Our plot indicates that out of the 2 to 4 cluster solutions, a three cluster solution has the highest median ARI out of 5 runs.

Now, after deciding on a suitable number of clusters, we could select the corresponding cluster solution from kcca or stepFlexclust, and make use of the further visualization, prediction, and other tools. For this, we refer to the documentation available in Leisch (2006) and Dolnicar, Grün, and Leisch (2018).

Model-based approach

We also offer an algorithm specifically designed for model-based clustering of unordered categorical data via a regularized multinomial distribution. The multinomial driver also supports varying number of categories between variables. We call flexmix using the model driver FLXMCregmultinom() where we specify via the argument r the number of categories for each variable:

titanic_ncats <- apply(titanic_dm, 2, max)
flexmix(formula = titanic_dm ~ 1, k = 3,
        model = FLXMCregmultinom(r = titanic_ncats)) 
#> 
#> Call:
#> flexmix(formula = titanic_dm ~ 1, k = 3, model = FLXMCregmultinom(r = titanic_ncats))
#> 
#> Cluster sizes:
#>    1    2    3 
#> 1208  364  629 
#> 
#> convergence after 125 iterations

As we are estimating many category probabilities across multiple clusters, some of those may become numerically zero, resulting in a degenerate distribution. To avoid this we may use the regularization parameter \(\alpha\), which acts if we added \(\alpha\) observations according to the population mean to each component:

flexmix(titanic_dm ~ 1, k = 3,
        model = FLXMCregmultinom(r = titanic_ncats, alpha = 1))
#> 
#> Call:
#> flexmix(formula = titanic_dm ~ 1, k = 3, model = FLXMCregmultinom(r = titanic_ncats, 
#>     alpha = 1))
#> 
#> Cluster sizes:
#>    1    2    3 
#>  364  629 1208 
#> 
#> convergence after 56 iterations

flexmix also provides function stepFlexmix(), where the EM algorithm for each k is restarted nrep times, and only the maximum likelihood solution is retained:

(nom <- stepFlexmix(titanic_dm ~ 1, k = 2:4,
                    nrep = 3, # please increase for real-life use
                    model = FLXMCregmultinom(r = titanic_ncats)))
#> 2 : * * *
#> 3 : * * *
#> 4 : * * *
#> 
#> Call:
#> stepFlexmix(titanic_dm ~ 1, model = FLXMCregmultinom(r = titanic_ncats), 
#>     k = 2:4, nrep = 3)
#> 
#>   iter converged k k0    logLik      AIC      BIC      ICL
#> 2   38      TRUE 2  2 -5327.340 10680.68 10754.74 10986.90
#> 3  103      TRUE 3  3 -5202.816 10445.63 10559.57 11036.09
#> 4  121      TRUE 4  4 -5176.038 10406.08 10559.89 11454.98

The output provides an overview on the best solutions out of three EM runs for 3 different values of k. For each solution, it is indicated how many iterations of the EM algorithm were performed (iter), if the EM algorithm converged (converged), the number of components in the final solution (k) and the number of components the EM algorithm was initialized with (k0) as well as the maximum log-likelihood (logLik) and results for different model selection criteria, namely, AIC, BIC and ICL.

Similar to package flexclust in the partitioning case, package flexmix also offers various plotting methods for the returned objects. We just showcase here one:

plot(nom)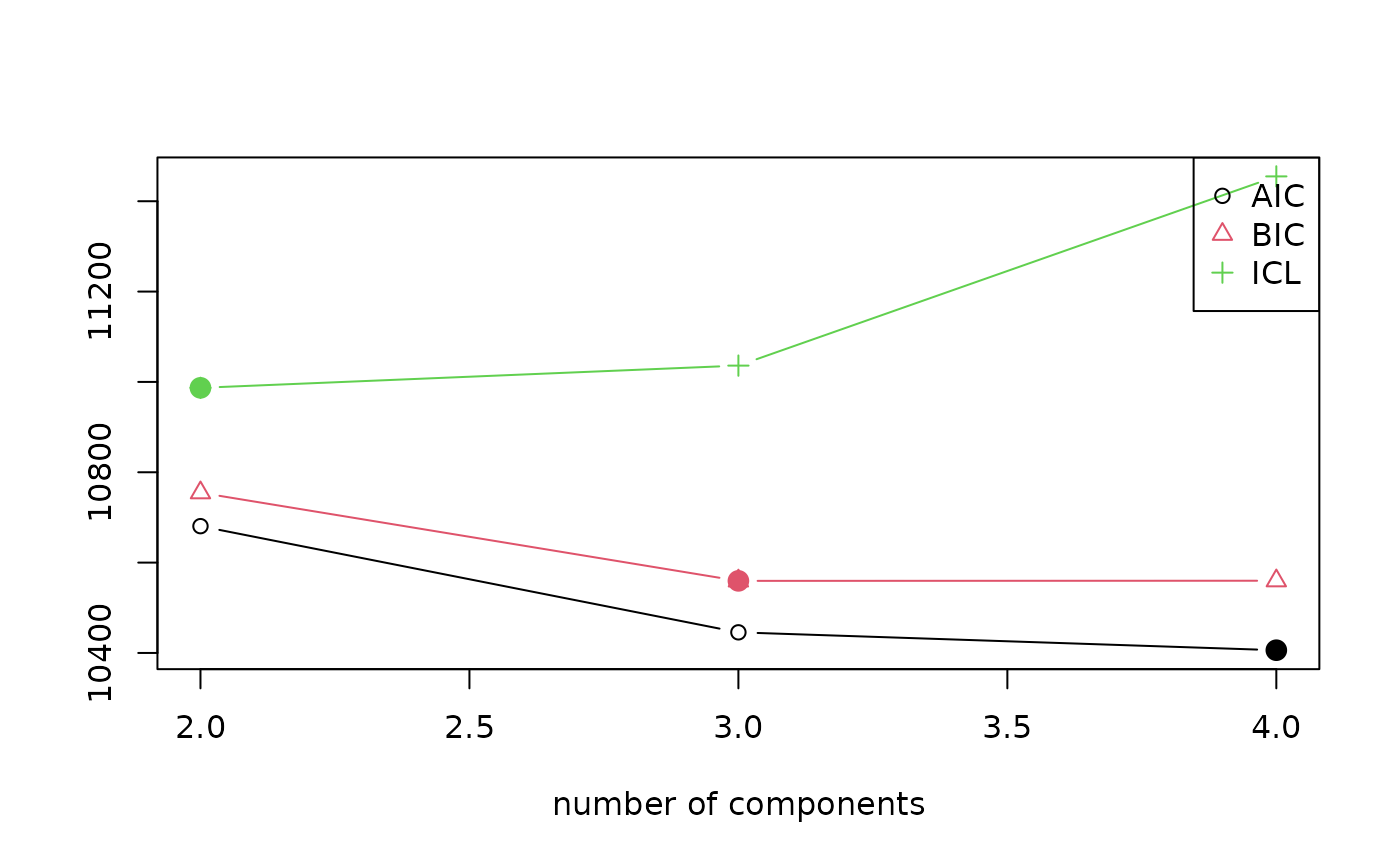

For more information on the further methods and utilities offered, check out the documentation for flexmix (see for example browseVignettes('flexmix')).

Example 2: Clustering purely ordinal data

Our next example data set is from a survey conducted among 563 Australians in 2015 where they indicated on a scale from 1-5 how inclined they are to take 6 types of risks. It consists of purely ordinal variables without missing values, and the response level length is the same for all variables. We load the data set and inspect it:

data("risk", package = "flexord")
str(risk)
#>  int [1:563, 1:6] 3 1 2 1 5 5 1 5 1 3 ...
#>  - attr(*, "dimnames")=List of 2
#>   ..$ : NULL
#>   ..$ : chr [1:6] "Recreational" "Health" "Career" "Financial" ...
colnames(risk)
#> [1] "Recreational" "Health"       "Career"       "Financial"    "Safety"      
#> [6] "Social"

Partitioning approach

In our package, we offer two partitioning methods designed for ordinal data based on either Gower’s distance or GDM2 distance.

Applying Gower’s distance as implemented in distGower to purely ordinal data corresponds to using Manhattan distance (as provided also in flexclust::distManhattan) with previous scaling as described by Kaufman and Rousseeuw (1990) and Gower’s upweighing of non-missing values. The clustering can be performed using:

kcca(risk, k = 3, family = kccaExtendedFamily('kGower'))
#> kcca object of family 'kGower' 
#> 
#> call:
#> kcca(x = risk, k = 3, family = kccaExtendedFamily("kGower"))
#> 
#> cluster sizes:
#> 
#>   1   2   3 
#> 161 131 271

The default centroid for this family is the general purpose optimizer centOptimNA, which is the general purpose optimizer flexclust::centOptim, just with NA removal. In our case of purely ordinal data with no missing values, we could also choose the median as a centroid:

kcca(risk, k = 3,
     family = kccaExtendedFamily('kGower', cent = centMedian))
#> kcca object of family 'kGower' 
#> 
#> call:
#> kcca(x = risk, k = 3, family = kccaExtendedFamily("kGower", cent = centMedian))
#> 
#> cluster sizes:
#> 
#>   1   2   3 
#> 303 160 100

This results in kMedians with previous scaling, and non-missing value upweighing. In our risk example with no NAs and equal response level lengths for all variables, flexclust::kccaFamily('kmedians') would suffice, but there are still many data situations where the "kGower" approach will be preferable.

As a second alternative designed specifically for ordinal data without missing values, we implement the GDM2 distance for ordinal data suggested by Walesiak and Dudek (2010), which conducts only relational operations on ordinal variables. We reformulated this distance for use in K-centroids clustering in Ernst et al. (2025), and implemented it in the package such that one can use it for clustering via:

kcca(risk, k = 3, family = kccaExtendedFamily('kGDM2'))
#> kcca object of family 'kGDM2' 
#> 
#> call:
#> kcca(x = risk, k = 3, family = kccaExtendedFamily("kGDM2"))
#> 
#> cluster sizes:
#> 
#>   1   2   3 
#> 342  97 124

Similar to "kGower", a default general optimizer centroid is applied, which we could replace as desired.

Another parameter used in both "kGower" and "kGDM2" is xrange. Both algorithms require information on the range of the variables of the data object for data pre-processing: "kGower" uses this for scaling, while "kGDM2" for transforming the data to empirical distributions. The range calculation can be influenced in the following ways: We can use the range of the whole x (argument all, the default for "kGDM2"), columnwise ranges (xrange = "columnwise"), a vector specifying the range across all variables in the data set, or a list of length ncol(x) with range vectors for each column. Let us assume that the highest possible response to the risk questions was Extremely often (6), but it was never chosen by any of the respondents. We can take the new assumed full range of the data into account:

kcca(risk, k = 3,
     family = kccaExtendedFamily('kGDM2', xrange = c(1, 6)))
#> kcca object of family 'kGDM2' 
#> 
#> call:
#> kcca(x = risk, k = 3, family = kccaExtendedFamily("kGDM2", xrange = c(1, 
#>     6)))
#> 
#> cluster sizes:
#> 
#>   1   2   3 
#> 117  97 349

Again, the distances, centroids, and wrapper alternatives presented can be used also in the further capabilities of flexclust.

Model-based approach

We also offer model drivers for two component distributions suitable for ordinal data, which are the binomial distribution and its extension the beta-binomial distribution:

risk1 <- risk - 1
flexmix(risk1 ~ 1, k = 3, model = FLXMCregbinom(size = 4))
#> 
#> Call:
#> flexmix(formula = risk1 ~ 1, k = 3, model = FLXMCregbinom(size = 4))
#> 
#> Cluster sizes:
#>   1   2   3 
#>  43 401 119 
#> 
#> convergence after 69 iterations
flexmix(risk1 ~ 1, k = 3, model = FLXMCregbetabinom(size = 4, alpha = 1))
#> 
#> Call:
#> flexmix(formula = risk1 ~ 1, k = 3, model = FLXMCregbetabinom(size = 4, 
#>     alpha = 1))
#> 
#> Cluster sizes:
#>   1   2   3 
#>  49 108 406 
#> 
#> convergence after 89 iterations

In both cases we specify the number of trials of the binomial distribution (size). For both distributions we can also use a regularization parameter alpha that shrinkgs the component estimates towards the population mean. While this incurs small distortions it can be helpful to avoid boundary estimates.

The beta-binomial distribution is parameterized by two parameters a and b and is therefore more flexible than the binomial. It may potentially perform better in more difficult clustering scenarios even if we assume the original data was drawn from a binomial mixture (Ernst et al. 2025). Your mileage may vary.

We can further use the capabilities of stepFlexmix and the corresponding plot functions.

Treating the data as purely nominal

Treating ordered categorical data as unordered is a frequent approach. In fact, in our simulation study it was a quite competitive approach for model-based methods. However, applying kmodes to ordered data brought subpar results in the partitioning ambit (Ernst et al. 2025).

Treating the data as equidistant (=integer)

Also treating ordered categorical data as integer values is at least as common as nominalization. In fact, some of the methods presented above, such as "kGower" - as used above on purely ordinal data without missing values - make only lax concessions towards ordinality. Depending on data characteristics and specific method applied, this approach may also be a very good choice (Ernst et al. 2025).

We do not offer any new methods for this in the partitioning ambit, as already many options are available in flexclust. In the model-based ambit we offer additional capabilities via FLXMCregnorm, which, as mentioned, is a driver for clustering with multivariate normal distributions (assuming conditional independence) while allowing for regularization (as in the case for FLXMCregmultinom to help avoid degenerate solutions). One can proceed as follows to use the data-driven default regularization parameters as proposed by Fraley and Raftery (2007):

params <- FLXMCregnorm_defaults(risk, kappa_p = 0.1, k = 3)
flexmix(risk ~ 1, k = 3, model = FLXMCregnorm(params = params))
#> 
#> Call:
#> flexmix(formula = risk ~ 1, k = 3, model = FLXMCregnorm(params = params))
#> 
#> Cluster sizes:
#>   1   2 
#>  58 505 
#> 
#> convergence after 51 iterations

For details on the parameters used for regularization, see Fraley and Raftery (2007) or package mclust. Here, we would only like to point out that the shrinkage parameter kappa_p (the suffix _p stands for prior), acts as if we added kappa_p observations according to the population mean to each component. Using FLXMCregnorm_defaults with the data and the number of components determines the scale parameter zeta_p by dividing the empirical variance by the square of the number of components. Thus we need to pass the data and k = 3. Alternatively, we could also specify a value for zeta_p and then omit the parameter k. Note that we cannot set both parameters at the same time and therefore, zeta_p takes precedence if both are given.

Again, the model can be plugged into all of the further tools offered by flexmix.

Example 3: Clustering mixed-type data with missing values 

data("vacmot", package = "flexclust")
vacmot2 <- cbind(vacmotdesc,
                 apply(vacmot, 2, as.logical))
vacmot2 <- vacmot2[, c('Gender', 'Age', 'Income2', 'Relationship.Status', 'Vacation.Behaviour',
                       sample(colnames(vacmot), 3, replace = FALSE))]
vacmot2$Income2 <- as.ordered(vacmot2$Income2) 
str(vacmot2)
#> 'data.frame':    1000 obs. of  8 variables:
#>  $ Gender                  : Factor w/ 2 levels "Male","Female": 2 2 1 2 1 2 1 1 2 2 ...
#>  $ Age                     : num  25 31 21 18 61 63 58 41 36 56 ...
#>  $ Income2                 : Ord.factor w/ 5 levels "<30k"<"30-60k"<..: 2 5 4 2 1 2 1 2 4 2 ...
#>  $ Relationship.Status     : Factor w/ 5 levels "single","married",..: 1 2 1 1 2 2 3 4 3 2 ...
#>  $ Vacation.Behaviour      : num  2.07 2 1.23 2.17 1.72 ...
#>  $ realise creativity      : logi  FALSE FALSE FALSE FALSE FALSE FALSE ...
#>  $ rest and relax          : logi  TRUE TRUE TRUE TRUE TRUE TRUE ...
#>  $ entertainment facilities: logi  FALSE FALSE FALSE TRUE FALSE FALSE ...
colMeans(is.na(vacmot2))*100 
#>                   Gender                      Age                  Income2 
#>                      0.0                      0.0                      6.6 
#>      Relationship.Status       Vacation.Behaviour       realise creativity 
#>                      0.4                      2.5                      0.0 
#>           rest and relax entertainment facilities 
#>                      0.0                      0.0

For our last example, we use a data set which is obtained by merging two data sets shared in package flexclust. flexclust provides object vacmot consisting of a \(1000 \times 20\) matrix of binary responses to questions on travel motives asked Australian tourists in 2006, plus a separate data frame vacmotdesc with 12 demographic variables for each respondent.

This data set has been thoroughly explored using clustering methods in the field of market segmentation research, see for example Dolnicar and Leisch (2008). We now use it as a data example for a mixed-data case with a moderate amount of missingness. For this, we select one symmetric binary variable (Gender, which was collected as Male/Female in 2006), two numeric variables (Age and Vacation Behaviour3), one unordered categorical variable (Relationship Status), one ordered categorical variable (Income2, which is a recoding of Income), and three randomly selected asymmetric binary variables (3 of the 20 questions on whether a specific travel motive applies to a respondent). Missing values are present, but the percentage is low4.

Partitioning approach

Currently, we only offer one method for mixed-type data with missing values, which is "kGower" (scaling and distances as proposed by Gower (1971) and Kaufman and Rousseeuw (1990), and a general purpose optimizer centroid as provided in flexclust, but with NA omission):

kcca(vacmot2, k = 3, family = kccaExtendedFamily('kGower'))
#> kcca object of family 'kGower' 
#> 
#> call:
#> kcca(x = vacmot2, k = 3, family = kccaExtendedFamily("kGower"))
#> 
#> cluster sizes:
#> 
#>   1   2   3 
#> 535  92 373

In our example above, the default methods for each variable type are used (Simple Matching Distance for the categorical variables, squared Euclidean distance for the numerical/integer variables, Manhattan distance for ordinal variables, and Jaccard distance for logical variables).

We could instead provide a vector of length ncol(vacmot2) where each distance measure to be used is specified. Let us assume that we have many outliers in the variable Age, that we woud like to consider Vacation.Behaviour an ordered factor as well in addition to Income2, and that the three binary responses to vacation motives should be treated symmetric instead of asymmetric5, and for this reason want to evaluate the first three with Manhattan distance, and the latter three with Euclidean distance6:

colnames(vacmot2)
#> [1] "Gender"                   "Age"                     
#> [3] "Income2"                  "Relationship.Status"     
#> [5] "Vacation.Behaviour"       "realise creativity"      
#> [7] "rest and relax"           "entertainment facilities"
xmthds <- c('distSimMatch', rep('distManhattan', 3),
            'distSimMatch', rep('distEuclidean', 3))
kcca(vacmot2, k = 3,
     family = kccaExtendedFamily('kGower', xmethods = xmthds))
#> kcca object of family 'kGower' 
#> 
#> call:
#> kcca(x = vacmot2, k = 3, family = kccaExtendedFamily("kGower", 
#>     xmethods = xmthds))
#> 
#> cluster sizes:
#> 
#>   1   2 
#> 488 512

For "kGower", all numeric/integer and ordered variables are scaled as proposed by Kaufman and Rousseeuw (1990), by shifting by the minimum and dividing by the range. This means that also for "kGower", the range of the variables will influence the clustering results. Same as for "kGDM2" (Example 2), we can specify the range to be used in parameter xrange. In the case of "kGower", the default value is "columnwise", where the range for each column is calculated separately.

Again, the distance, centroid and wrapper functions can be used in the further tools provided by flexclust, for examples on that see Example 1.

References

Dolnicar, Sara, Bettina Grün, and Friedrich Leisch. 2018. Market Segmentation Analysis. Management for Professionals. Singapore: Springer-Verlag. https://doi.org/10.1007/978-981-10-8818-6_2.
Dolnicar, Sara, and Friedrich Leisch. 2008. “An Investigation of Tourists’ Patterns of Obligation to Protect the Environment.” Journal of Travel Research 46 (4): 381–91. https://doi.org/10.1177/0047287507308330.
Ernst, Dominik, Lena Ortega Menjivar, Theresa Scharl, and Bettina Grün. 2025. “Ordinal Clustering with the Flex-Scheme.” Austrian Journal of Statistics.
Fraley, Chris, and Adrian E Raftery. 2007. “Bayesian Regularization for Normal Mixture Estimation and Model-Based Clustering.” Journal of Classification 24 (2): 155–81. https://doi.org/10.1007/s00357-007-0004-5.
Galindo Garre, Francisca, and Jeroen K Vermunt. 2006. “Avoiding Boundary Estimates in Latent Class Analysis by Bayesian Posterior Mode Estimation.” Behaviormetrika 33: 43–59. https://doi.org/10.2333/bhmk.33.43.
Gower, J. C. 1971. “A General Coefficient of Similarity and Some of Its Properties.” Biometrics 27 (4): 857–71. https://doi.org/10.2307/2528823.
Hubert, Lawrence, and Phipps Arabie. 1985. “Comparing Partitions.” Journal of Classification 2 (1): 193–218. https://doi.org/10.1007/BF01908075.
Kaufman, Leonard, and Peter Rousseeuw. 1990. Finding Groups in Data: An Introduction to Cluster Analysis. Wiley Series in Probability and Statistics. New York: John Wiley & Sons. https://doi.org/10.1002/9780470316801.
Kondofersky, Ivan. 2008. “Modellbasiertes Clustern mit Der Beta-Binomialverteilung.” Bachelor's Thesis.
Leisch, Friedrich. 2006. “A Toolbox for K-Centroids Cluster Analysis.” Computational Statistics & Data Analysis 51 (2): 526–44. https://doi.org/10.1016/j.csda.2005.10.006.
Walesiak, Marek, and Andrzej Dudek. 2010. “Finding Groups in Ordinal Data: An Examination of Some Clustering Procedures.” In Classification as a Tool for Research, edited by Hermann Locarek-Junge and Claus Weihs, 185–92. Berlin, Heidelberg: Springer-Verlag. https://doi.org/10.1007/978-3-642-10745-0_19.
Weihs, Claus, Uwe Ligges, Karsten Luebke, and Nils Raabe. 2005. “klaR Analyzing German Business Cycles.” In Data Analysis and Decision Support, edited by Daniel Baier, Reinhold Decker, and Lars Schmidt-Thieme, 335–43. Berlin: Springer-Verlag. https://doi.org/10.1007/3-540-28397-8_36.

  1. Internally, it will be converted to a data.matrix. However, as only equality operations and frequency counts are used, this is of no consequence.↩︎

  2. I.e., the mean disagreement count.↩︎

  3. Mean environmental friendly behavior score, ranging from 1 to 5.↩︎

  4. This is by choice. While Gower’s distance is designed to handle missingness via variable weighting, and the general optimizer used here is written to omit NAs, both methods will degenerate with high percentages of missing values. While we have not yet determined the critical limit, we have successfully run the algorithm on purely ordinal data with MCAR missingness percentages of up to 30%. However, common sense dictates that solutions obtained for such high missingness percentages need to be treated with caution.↩︎

  5. Meaning that 2 disagreements are just as important as 2 agreements.↩︎

  6. We could achieve symmetric treatment also via Simple Matching Distance.↩︎